PERFIL
BIOGRÁFICO Y ACADÉMICO
Nacido
en Petoskey, Michigan (Estados Unidos), hijo del juez de
Gaylord y una profesora de secundaria. Desde su juventud
se destacó por su inquietud investigadora y su habilidad
en la creación de prototipos técnicos, tal
vez dando continuidad al talento creativo de su abuelo.
Se graduó con premio extraordinario en la Universidad
de Michigan en Ingeniería Eléctrica y en
Matemáticas.
A los 20 años se trasladó al Instituto Tecnológico de Massachusetts (MIT) como ayudante de investigación en ingeniería eléctrica, donde superó, a los 24 años, su tesis doctoral en matemáticas sobre la aplicación del álgebra ‘booleana’ en el análisis de datos (An Algebra for Theoretical Genetics). En el MIT se ocupó en el desarrollo de los primeros ordenadores, cerca de Vannevar Bush, cuyo ‘Memex’ ha sido considerado un claro antecedente de Internet.
A los 25 años publica Mathematical theory of the differential analyzer. También trabajó en los Laboratorios Bell y en el Institute for Advanced Study de Princenton en sistemas de automatización de armas.
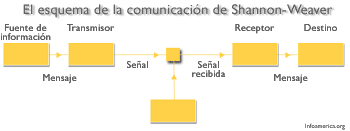
Pero su trabajo central no aparecerá hasta 1948, cuando presenta su Teoría Matemática de la Comunicación, un trabajo que ha sido calificado como la ‘carta magna’ de la era de la información (`A Mathematical Theory of Communication', Bell System Technical Journal, Vol. 27, julio y octubre 1948, págs. 379-423 y 623-656, que un año más tarde revisa, en un trabajo enriquecido por Warren Weaver, bajo el enunciado de The Mathematical Theory of Communication, publicado por la Universidad de Illinois). Asimismo se da a conocer el teorema Shannon-Hartley, según el cual sólo es posible eliminar el 'ruido' en la transmisión de información cuando el flujo de información no exceda la capacidad del canal.
La biografía de Shannon está llena de los frutos de su ingenio, con numerosas aplicaciones en el campo de las máquinas automáticas, desde un ratón electrónico hasta un WC automático, pasando por diversos juego electrónicos de ajedrez, calculadoras, instrumentos musicales, juguetes mecánicos, relojes, etc.
Miembro de la Academia Americana de Artes y Ciencias, de la Academia Nacional de Ciencias, de la Academia Nacional de Ingeniería, de la Sociedad Filosófica Americana y la Royal Society de Londres. Entre los numerosos premios recibidos por Shannon, destacan la National Medal of Science en 1966, el Kyoto en 1985, etcétera.
A los 20 años se trasladó al Instituto Tecnológico de Massachusetts (MIT) como ayudante de investigación en ingeniería eléctrica, donde superó, a los 24 años, su tesis doctoral en matemáticas sobre la aplicación del álgebra ‘booleana’ en el análisis de datos (An Algebra for Theoretical Genetics). En el MIT se ocupó en el desarrollo de los primeros ordenadores, cerca de Vannevar Bush, cuyo ‘Memex’ ha sido considerado un claro antecedente de Internet.
A los 25 años publica Mathematical theory of the differential analyzer. También trabajó en los Laboratorios Bell y en el Institute for Advanced Study de Princenton en sistemas de automatización de armas.
Pero su trabajo central no aparecerá hasta 1948, cuando presenta su Teoría Matemática de la Comunicación, un trabajo que ha sido calificado como la ‘carta magna’ de la era de la información (`A Mathematical Theory of Communication', Bell System Technical Journal, Vol. 27, julio y octubre 1948, págs. 379-423 y 623-656, que un año más tarde revisa, en un trabajo enriquecido por Warren Weaver, bajo el enunciado de The Mathematical Theory of Communication, publicado por la Universidad de Illinois). Asimismo se da a conocer el teorema Shannon-Hartley, según el cual sólo es posible eliminar el 'ruido' en la transmisión de información cuando el flujo de información no exceda la capacidad del canal.
La biografía de Shannon está llena de los frutos de su ingenio, con numerosas aplicaciones en el campo de las máquinas automáticas, desde un ratón electrónico hasta un WC automático, pasando por diversos juego electrónicos de ajedrez, calculadoras, instrumentos musicales, juguetes mecánicos, relojes, etc.
Miembro de la Academia Americana de Artes y Ciencias, de la Academia Nacional de Ciencias, de la Academia Nacional de Ingeniería, de la Sociedad Filosófica Americana y la Royal Society de Londres. Entre los numerosos premios recibidos por Shannon, destacan la National Medal of Science en 1966, el Kyoto en 1985, etcétera.
PENSAMIENTO
Y EXPRESIÓN CIENTÍFICA Al cabo de más de medio siglo de sus hallazgos se sigue considerando el trabajo de Shannon
la
pieza clave en el desarrollo que lleva a que la comunicación
adquiera un carácter de centralidad en la sociedad
actual. Asimismo, sienta los fundamentos matemáticos
de la revolución tecnológica de la segunda
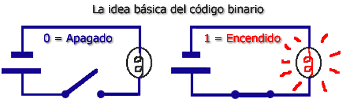
mitad del siglo XX.Desde el estudio del álgebra 'booleana' teoriza acerca del código binario, la base del lenguaje digital, a partir de unidades básicas de información, definidas por dos estados: el ‘si’ y el ‘no’, el 0 y el 1, abierto/cerrado, verdadero/falso, blanco/negro. El 0 y el 1 aparecen como el átomo de la información, como la base constructiva del mensaje. Una información compleja es una sucesión de unidades básicas, de unos y ceros. Más allá de la formulación teórica, Shannon construyó circuitos y máquinas basadas en los flujos binarios de información, mediante interruptores y relés en las que se anticipaban los embriones de muchos de los desarrollos de las décadas posteriores.
